The answer is easy: Waves are solutions to the wave equation - big deal.
Signals are propagating discontinuities determined by the point sets for which
the solutions to the wave equation are not uniquely defined. - that is a truely
big deal.
There are three equivalence classes of signals.
- Longitudinal (real functions)
- Transverse (Complex functions)
- Torsion or Spinor waves (actually two species)
The eikonal is the characteristic equation which determines the point sets upon
which solutions to the wave equation are not uniquely defined. These point
sets are not necessarily stationary. They can propagate. The fundamental idea is
that there is a wave equation and TWO species of the eikonal equation. These
propagating discontinuities are defined as signals.
One species of eikonal equation is a quadratic form that has the signature
{+++, - } relative to {x,y,z, t}. The second eikonal equation is a quadratic
form that has the signature {---, + } relative to {x,y,z, t}. Now that does
not seem like a big difference, for one is just the negative of the other.
BUT--
The first is related to the set of symbols {E I J K} where the last three symbols have a composition rule [I,J]=>K with cyclic permutations, but where the structural constraint I^2 = J^2 = K^2 = 1. and E^2 = -1.
The second is related to the set of symbols {1 I J K} where the last three
symbols have a composition rule [I,J]=>K with cyclic permutations, but where
the structural constraint I^2 = J^2 = K^2 = -1.
These objects form the generators of the Clifford Algebra (1,3) - one minus
sign, three plus signs - vs the Clifford algebra (3,1) - three minus signs, one
plus sign.
The Cl(1,3) is isomorphic to 4 x 4 matrices of real numbers. The Cl(3,1) is
isomorphic to 2 x 2 matrices of quaternions. BOTH representations will give a
different factorization of the eikonal equation into linear factors!
IN OTHER WORDS THERE ARE TWO TYPES OF PROPAGATING DISCONTINUITIES (SIGNALS) IN
SPACE TIME.
The Cl(1,3) types have been called Majorana spinors, while the Cl(3,1) types are most famous as Dirac spinors. The first have associations with the orthogonal group, while the second are associated with the Symplectic group.
Tony Smith has a great site on Clifford Algebras.
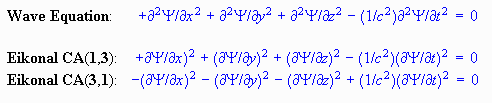ALT="image"> |
 |
As I have time I will replace this under construction symbol with a link to a more detailed pdf or tex file download. |