One of the things about projective geometry that has fascinated me for more than thirty years is the fact that all (projective) invariants are cross ratios (or functions thereof), and that except for special cases there exist six fundamental cross ratios for any configuration. The numeric values of the six cross ratios almost always fall into three classes:

1. The two cross ratios bounded by 1 and plus infinity,
2. The two cross ratios bounded by minus infinity and 0,
3. The two cross ratios bounded by 0 and 1.

The last class of numbers, bounded between zero and one, suggests a connection between these cross ratio invariants and the concepts of probability and statistics.
The concept is further strengthened by the recognition that Fermi's golden rule of transition probability is one of these cross ratios that is bounded by zero and 1.

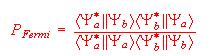
The question that arises is ''What is the physical significance and utility of the other projective invariant that is bounded between zero and 1, and what sort of probability does it represent? How are the two probabilities related (if at all)?

Recent suggestions by Valentini, and Abolhasani and Golshani (quant-ph/9707052), concerning the interesting idea of ''heat death''
(and brought to my attention via the Sarfatti net) have rekindled my interest in the possible utility of two types of ''projective'' probability.

Variations of the Cross Ratios.

In Projective geometry, a particular configuration exemplified by 4 lines in a plane intersecting at some perspective point p, generates 6 usually distinct cross ratios from the 4 points created by a fifth line arbitrarily intersecting all four lines. A similar result can be obtained from four planes intersecting at a common line, and then examining the rays created by a arbitrary plane that intersects the 4 original planes. Other examples can be created. When one cross ratio is evaluated with value k, the other cross ratios are known immediately, and have values (1-k), (1-1/k), 1/k,1/(1-k), and 1/(1-1/k).

A notable idea is that the six distinct cross ratios that can be constructed sometimes coalesce into pairs. The concept is related to the concept of degeneracy of eigen values in matrix algebra. That is, there exist certain configurations for which the cross ratios are degenerate. For example, if k = 1, the other (degenerate) cross ratios are 0 and infinity. In another example, if k = -1, the other degenerate cross ratios are 1/2 and 2. This case k = -1 is called a Harmonic cross ratio and has interesting properties. In particular, the two probabilities are equal at the harmonic limit.

In Figure 1. a schematic variation describes the values of the cross ratios between the two degenerate configurations where k= + 1 or k = -1. An arbitrary horizontal intercept yields the usual six values of the projective cross ratios between the two degeneracy limits, where the cross ratios coalesce in pairs.

Now suppose that the two xratios bounded between zero and 1 are related somehow to the Born probability, and the distribution probability, P, a la Valentini. In the degeneracy limit k = -1, the two probability limits are equal, so that their difference is zero. Does this correspond to the Valentini Heat Death limit? Note that the xratios are equal at k = 1/2 and k = 2 as well. Are these also "heat death" configurations

Another unanswered question is: What is the physical significance of the k = 1 limit ?
Does the physical projective system always evolve to the state of heat death? What is the functional relationship that would describe this evolutionary process?
Which curve is the Born probability and which curve is the distribution probability?

I will try to answer some of these questions in the future.
Any help is appreciated.