Falaco Solitons Click for a large picture

Falaco Solitons are exhibitions of topological defects in a discontinuity surface.
[ Kiehn 1986]. The phenomena is easily reproduced by placing a half-submerged circular disc (a Frisbee) in a swimming pool, then stroking the plate slowly in the direction of its oblate axis. At the end of the stroke extract the plate from the water, imparting kinetic energy and distributed angular momentum, to the fluid in the form of a pair of Rankine Vortices. In a few seconds, in bright sunlight, the concave Rankine depressions, with visible spiral arm caustics, will decay into a pair of convex dimples of negative Gauss curvature, which can be observed via their Snell projections as black spots on the bottom of the pool. In a few tries you will become an expert experimentalist, for the spots will persist for many minutes in a still pool.

Scroll down for The Optics of the Falaco Effect

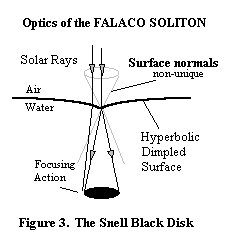
Falaco Solitons are long lived topological defects in the discontinuity free surface of water. They have remarkably long life times and will persist for 15 to 30 minutes. The black disks are created from the Snell refraction of a surface of rotational symmetry with negative Gauss curvature see Kiehn 1992.

The surface distortion is a pair of dimple-like depressions of a few millimeters. Unseen to the eye is a one dimensional defect or string that appears to connect the pair of surface two dimensional defects at their vertices. The stable shape of the connecting string is in the form of a circular arc.

The 1-dimensional defect, or string, is made visible by injecting dye drops near a dimple vertex. The dye drop executes helical transverse wave motion about the thread which acts as a guiding center. The dynamics is remindful of the action of whistler waves of charged particles executing helical motion along the earth's magnetic field line. The drop goes down, then back up, a number of times until finally the transverse helical motion sweeps out the entire circular arc connecting the two vertices.

If the string is dynamically severed, like the confinement problem for hadrons, the two surface defects (or Quarks!) cannot be separated. They disappear with a non-diffusive pop!

Download from LANL archive