|
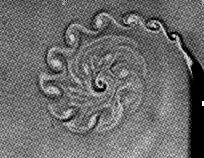
About 1990 it was established that the persistent scroll-like features of
visible wakes can be captured by a special subset of surfaces of tangential
discontinuities see Kiehn 1992 poitier.pdf.
The patterns, or surface structures, so formed are recognized by their
boundaries, which are interpreted as topological limit sets of instabilities
induced by fluctuations.
The Repere Mobile and Frenet Curvatures
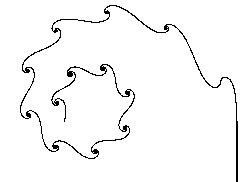
The morphology of the flow pattern on the left still illudes the most powerful
Cray computers. However, the pattern on the right was generated by a PC using
an analysis based on the Cartan-Frenet-Serret concept of the moving basis
frame or Repere Mobile. In the Frenet analysis the matrix of vectors
representing the basis frame at a moving point on a space curve is restricted to
be an element of the orthogonal group. Cartan ultimately extended this idea to
basis frames which belong to the projective group.
The key idea is that if a basis frame [F] has a global inverse,
[G], then the differential of any basis vector is closed with respect to
the original basis set. That is, the differential of any basis vector leads to
no surprises, and may be constructed in terms of linear combinations [C]
of the original basis frame.
When the tangential discontinuity is dominated by either Frenet curvature or Frenet torsion, the space curve is described by the complex phase equation
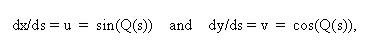
By choosing various formats for the phase function, Q(s), the morphology of most
wakes can be reproduced. The space curve is imbedded in a surface approximated
by a Minimal Surface.
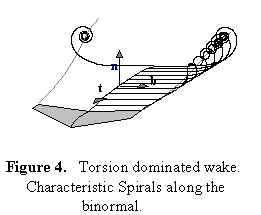
Lanchester Tip "Vortices"
When the wake is torsion dominated the appearance replicates the features of the
Lanchester theory of flight. The characteristic spirals of the phase function
form the tip vortices, which are the basis of drag on a wing of finite aspect
ratio. The spanwise spirals are mushrooms implying that the torsion is an even
function of spanwise arclength. The spirals dominated by curvature start from
the trailing edge and generate the Prandtl wake (not shown). The curvature is
an odd function of the arclength.
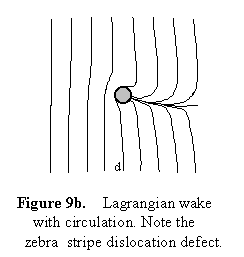
Lagrangian Wakes
Another aspect of wake phenomena is to be observed by comparing surfaces of
equal phase. In the translatory flow around a cylinder with circulation, but
without vorticity, the phase function of interest is generated by surfaces of
equal "time". In the figure at the right, these equal time surfaces connect
sequences of fluid elements with the same initial conditions. Note that the
circulation component of flow produces a defect in the equal time phase pattern.
Without circulation the defect disappears, and there is NO lift. The
system is described by a Cartan 1-form, A, which is closed, dA= 0. For any
smooth integration cycle around the cylinder, the circulation integral has a
finite value.
This result is in apparent contradiction to Stokes theorem, which, as the value
of vorticity is zero, would indicate that the circulation integral around a
closed integration path must be zero as well. However, Stokes theorem requires
that the integration chain be a boundary, and not just a cycle. For the flow
field with a harmonic component superposed upon a translational component, a
smooth curve around the origin is not a boundary in the topological sense. A
true boundary curve, consisting of two equal time segments above and below the
wing, and two flow line segments, does not cross the trailing edge defect line
transversly.
****
|